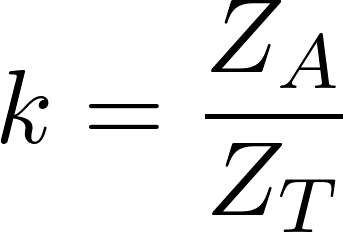
Quantifying Effectiveness
3 Minutes
2025-11-16
How can effectiveness be represented mathematically, specifically applied to airfoil profiles
This article is a summary of my thoughts on this topic
What does "effective" actually mean?
In everyday language, effectiveness is described as a large or good result achieved with little effort. But what does "large" or "good" mean? And what constitutes "little effort"? How exactly are these quantities represented mathematically? This is precisely what I'm trying to determine in order to later have a basis for evaluating my machine learning model for optimizing the airfoil.
Description of the quantity
In principle, effectiveness $k$ is the ratio between target values $Z_T$ and actual values $Z_A$.
$$k=\frac{Z_A}{Z_T}$$
In the following, I use effectiveness as a reward function and not in the classical sense.
Selection of quantities
Now the question arises: which quantities should be chosen as target and actual values? Essentially, we are looking for the quantities we want to maximize and those we want to minimize. A good starting point would be the ratio between lift $L$ and drag $D$
$$k = \frac{L}{D}$$
If we consider a larger value for $k$ to be positive, this can be achieved by striving for $L\rightarrow +\infty$ and $D\rightarrow 0$.
Environmental Effects
An aircraft is not a closed system.
Its impact on the environment must also be considered. When thinking about aircraft and their environmental impact, one probably immediately thinks of fuel consumption and noise, rather than the effect of the wings. However, the wings do contribute to the environmental effects.
The first thing that comes to mind is probably the noise generated. But how is noise quantified? We already have a unit for the loudness of sounds: the decibel. However, this unit has some properties that are counterproductive for calculating its effectiveness.
The decibel is on a logarithmic scale, unlike the physical quantities we have used so far. Therefore, the decibel is not particularly suitable as a unit of measurement.
One physical quantity suitable for representing both noise and other environmental effects is vorticity $\vec{\omega}$, which quantifies air turbulence. Air turbulence has no inherent qualitative property; to generate lift, the vorticity above the wing must be higher than the vorticity below it. However, higher vorticity also means more noise and a more turbelent way, which is why not only the magnitude of the vorticity but also the positions of the turbulences (also called vortices) must be considered.
Of course, vorticity alone is not responsible for lift.
In this phase of the project, the calculation of these quantities takes place in two-dimensional space, which is why I define three fields in which I want to measure the vorticity and either maximize or minimize it in each case.
- Minimize the value above the wing ($\vec{\omega_{a}}$)
- Maximize the value below the wing ($\vec{\omega_{b}}$)
- Minimize the value behind the wing ($\vec{\omega_{c}}$)
I understand that the vortices are all in the same vector field and therefore influence each other. However, I think these values are sufficient for a start and an approximation.
Conclusion
Now, all the values must be incorporated into the term describing the effectiveness. This will ultimately be a simple sum of simple fractions, since the value itself is not used in any further calculations; it simply rewards the machine learning model. Whether this will remain the only reward input is not yet clear.
$$ k = \frac{L}{D} + \frac{|\vec{\omega _a}|}{|\vec{\omega _b}|} + \frac{1}{|\vec{\omega _c}|}$$
Thanks for reading! :)
Sources
- Guyon, E., Hulin, J. P., Petit, L., & Mitescu, C. D. (2015). Physical hydrodynamics. Oxford university press.
- Engmann, K. (Ed.). (2013). Technologie des Flugzeuges. Vogel.